こちらの記事では倍電圧整流回路の設計方法について説明しております。
倍電圧整流回路を使用することにより、電源電圧を2倍以上にし、交流電源を直流に変換することが出来ます。
まず、回路の動作について説明した後に、各素子の定数と出力電圧との関係を確認し、
最後に実際の設計手順を説明します。
倍電圧整流回路の動作
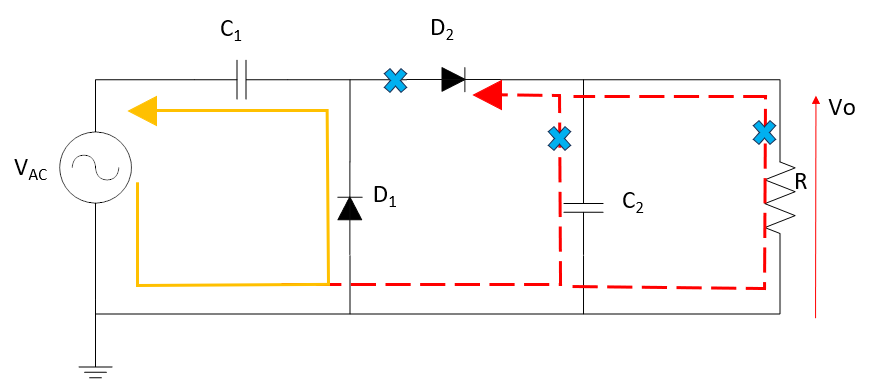
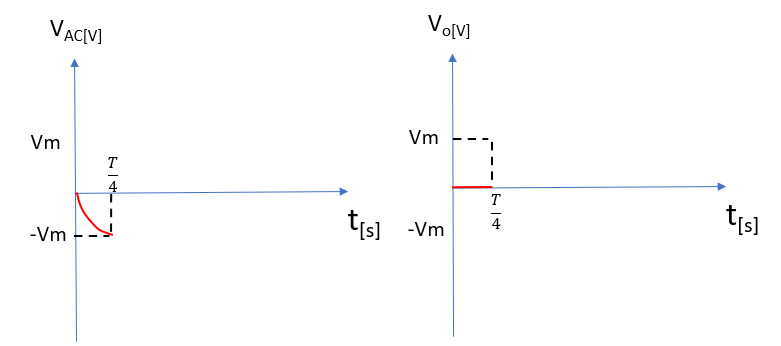
①時間tが0[s]~T/4[s]の時
電源の極性がマイナスのため、D1には順方向電圧がかかりD1→C1→電源の経路で電流が流れるため、
C1が充電される。D2には逆方向電圧がかかるため、C2やRには電流が流れない。
➁時間tがT/4[s]~T/2[s]の時
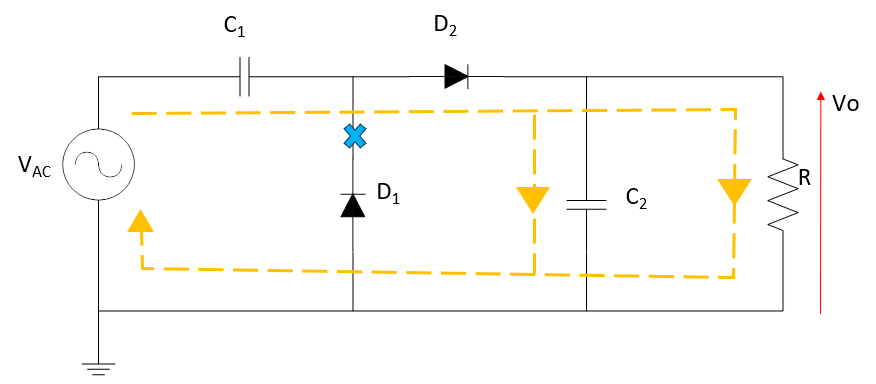
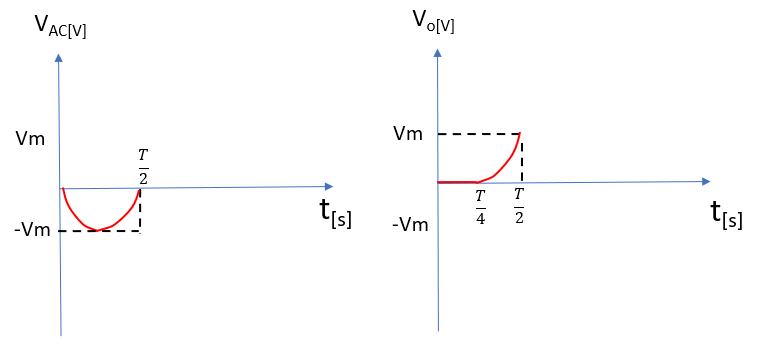
4/Tの時点でC1のコンデンサにはVmの電圧が充電されており、4/Tを過ぎると電源の瞬時値の絶対値が低下していくため、電源がマイナス方向に流そうとする力より、C1の放電でプラス側に流そうとする力が強くなる。
そのため、D1は逆方向電圧で電流が流れず、C2とRに電流が流れるようになる。これにより、C2は充電されていき、
Rにかかる電圧はC1の端子電圧と入力電圧の差分になるため2/T時点で電源の電圧が0Vになり、コンデンサの端子電圧Vmが負荷Rにかかる。
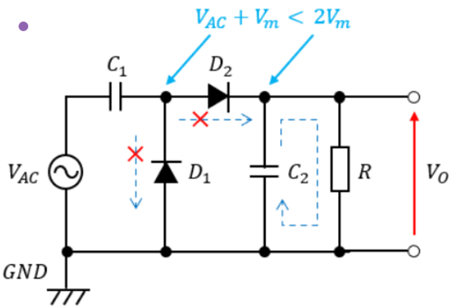
③時間tがT/2[s]~3T/4[s]の時

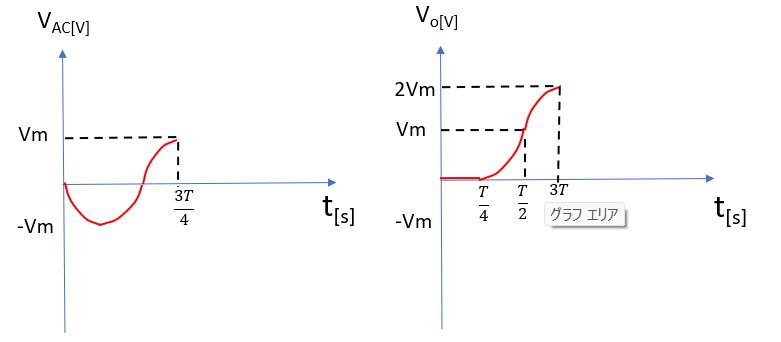
入力電圧がプラス側となるため、コンデンサC1の端子電圧と合計した電圧VAC+Vmが負荷Rに掛かる。
そして、3T/4時点で入力電圧もVmとなるため負荷Rに掛かる電圧はVm+Vm=2Vmで入力電圧の2倍となる。
そして、2VmがC2に掛かるのでC2も2Vm充電される。
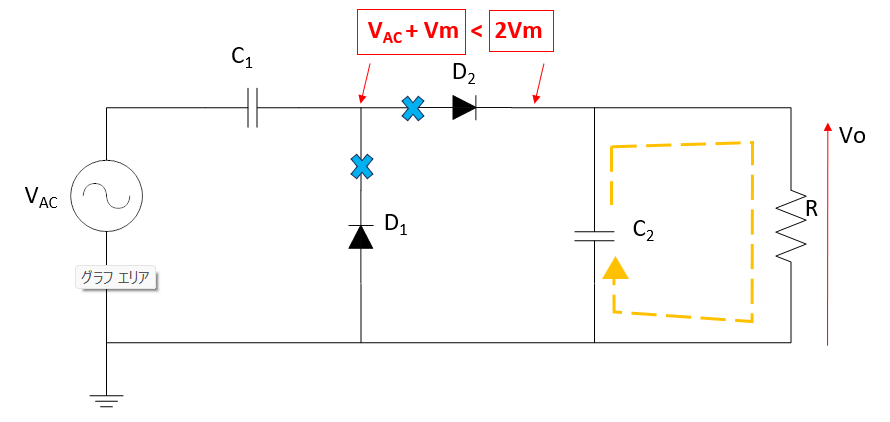
④時間tが3T/4[s]~T[s]の時
入力電圧がVmから0Vに向けて低下し始めると交流電源VAC+C1の端子電圧<C2の端子電圧となる。
これにより、D2のアノード側の電圧よりカソード側の電圧が大きいが、逆方向電圧となるため、
D2に電流は流れず、D1も逆方向電圧のため電流が流れない。
そのため、C2→Rの経路にのみ電流が流れていき、Rに掛かる電圧はC2の放電により徐々に減少していく。
この時のRに掛かる電圧の変化式はRC回路のため以下のようになる。
\(\ V_R=Ee^{-\frac{1}{CR}t}\)
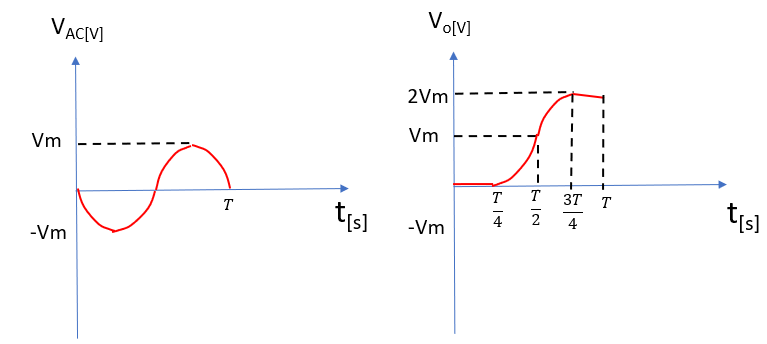
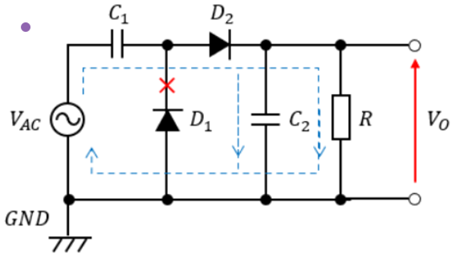
⑤時間tがT~T/4の時(2周期目以降)
時間tがT[s]以降は①~④を繰り返すが、C1とC2に電荷が残った状態になるため、
次の①T~T/4の時にはC2の放電が維持される。
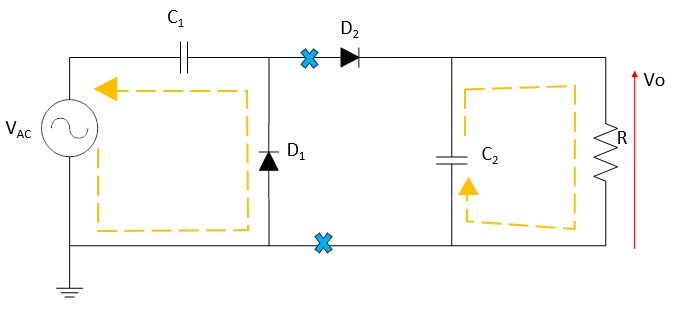
⑦T/4[s]~T/2[s]とT/2[s]~3T/4[s]の時(2周期目以降)
次の➁T/4[s]~T/2[s]と③T/2[s]~3T/4[s]の時は
「交流電源VAC+C1の端子電圧>C2の端子電圧」になるまではC2の放電を維持し、
「交流電源VAC+C1の端子電圧<C2の端子電圧」になったタイミングでC2は充電されるようになる。
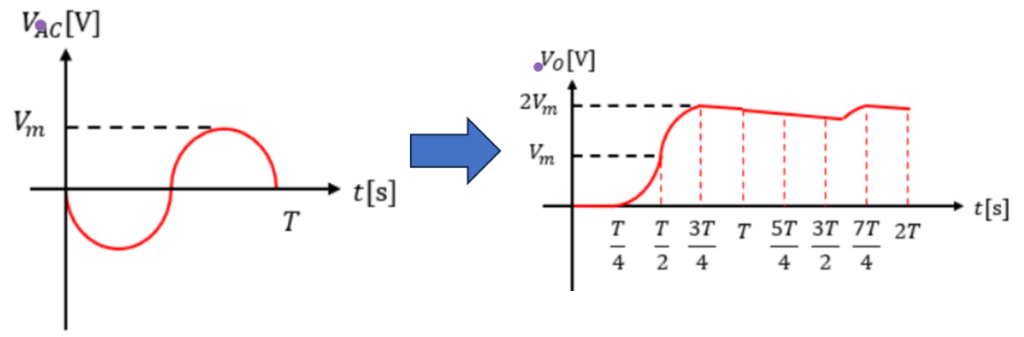
⑧結果
結果としては交流電源の入力電圧の約2倍の電圧値で維持される直流出力を得られる。
各素子の定数と出力電圧との関係
こちらではLTspiceを用いて回路内の各素子の定数が波形にどのような影響を及ぼしているかを確認する。
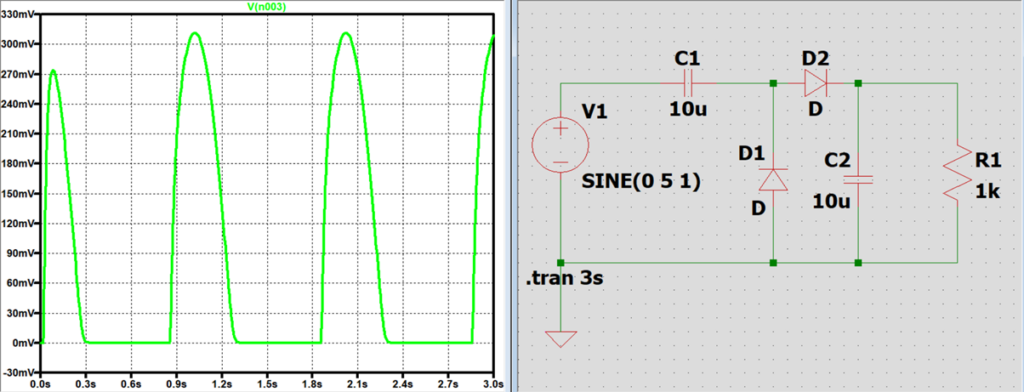
電源周波数と出力電圧の関係
電源周波数を高くするほど、電圧の増幅率が増加していき、電圧の振れ幅(偏差)が小さくなり、直流に近くなる。
これは周波数が高くなるほどコンデンサのインピーダンスが低くなり、回路に流れる電流量が多くなるため、
コンデンサが充放電する量が多くなり、結果として回路が安定していく。
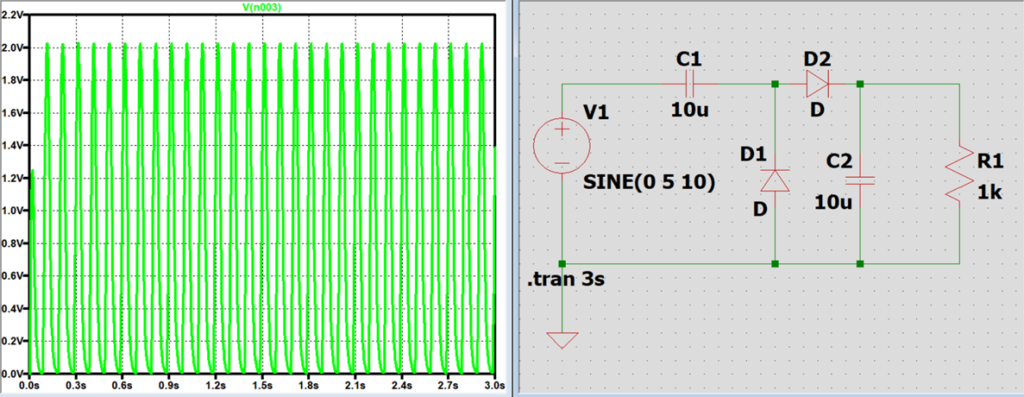

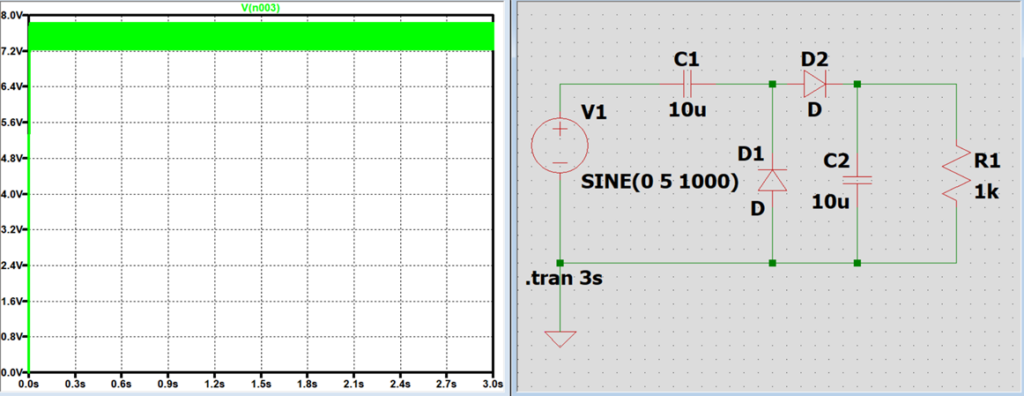
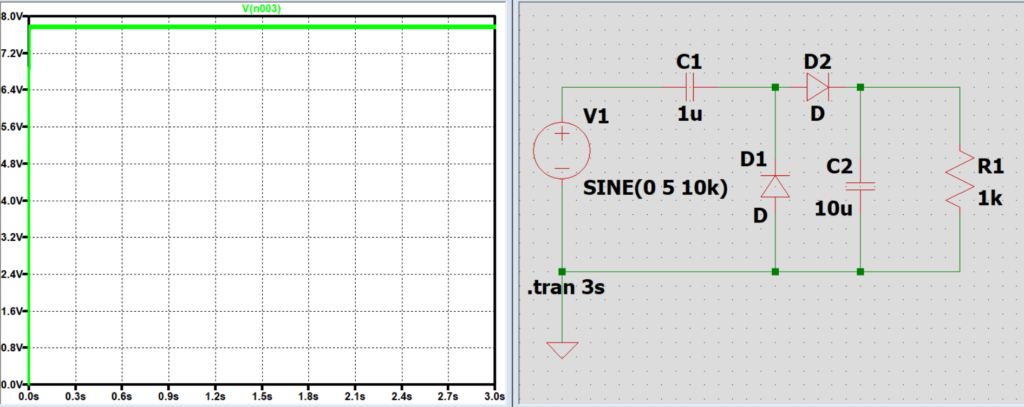
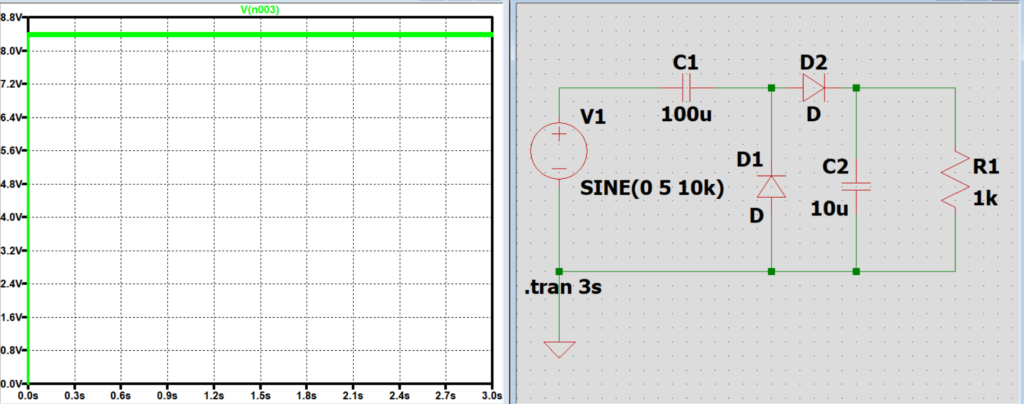
コンデンサC1の静電容量と出力電圧の関係
C1は電源と共に負荷に電圧を掛ける働きをしているため、負荷に掛かる電圧の大きさに影響を及ぼす。
C1が小さくなると放電時間が減少するため結果として負荷の電圧は小さくなり、
C1を大きくすると放電時間が増加するため結果として負荷の電圧は大きくなる。(限度値あり)
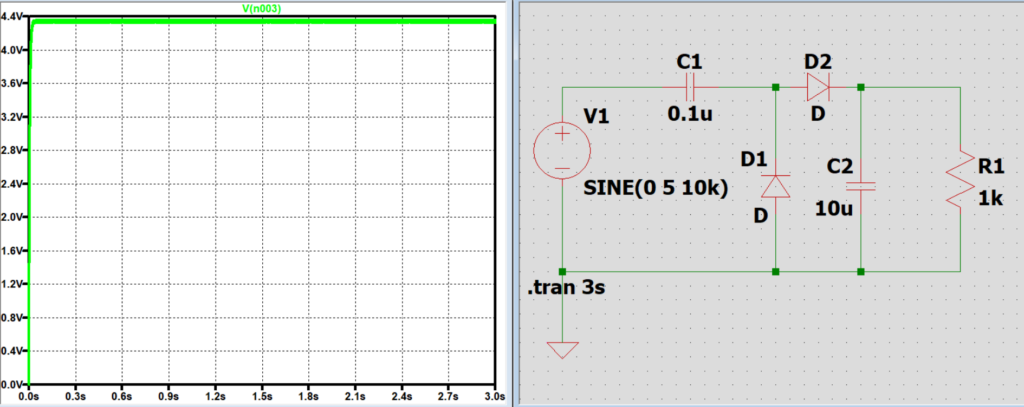
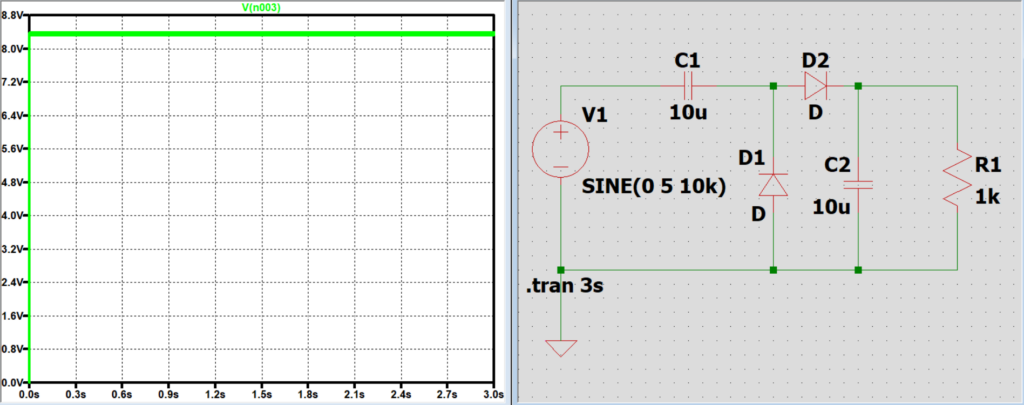
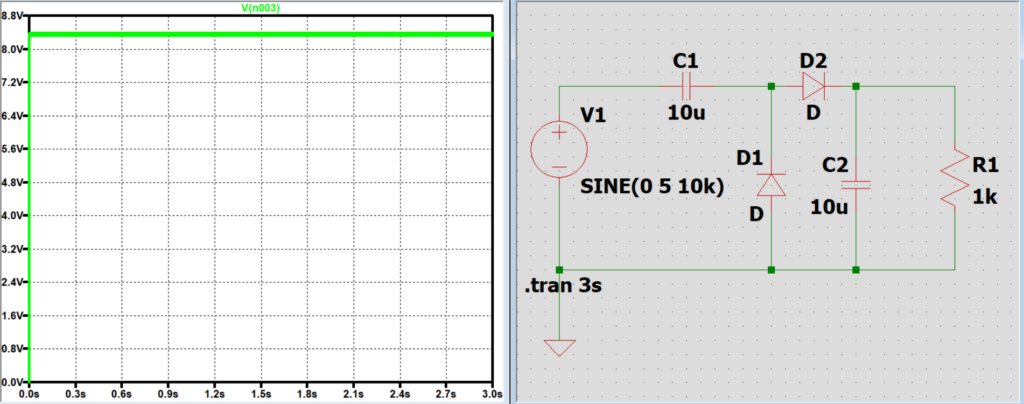
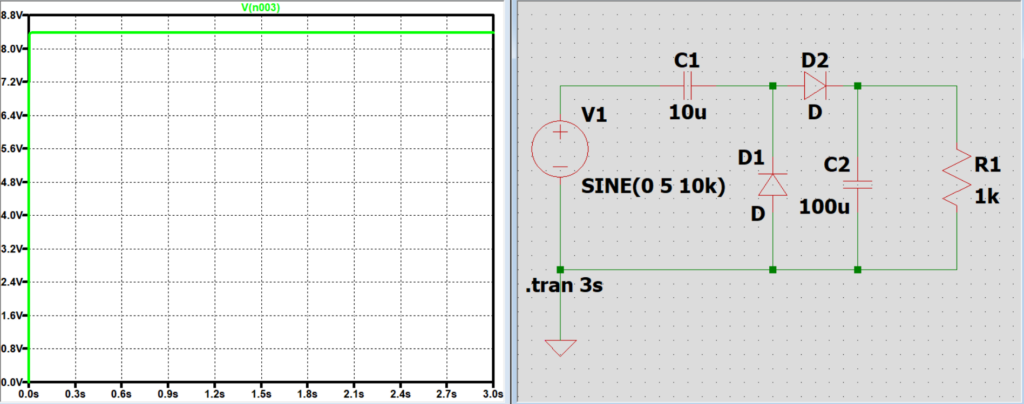
コンデンサC2の静電容量と出力電圧の関係
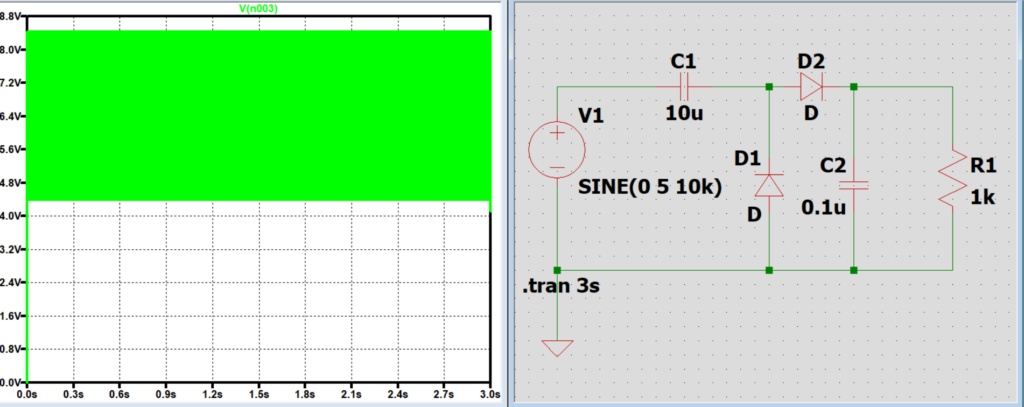
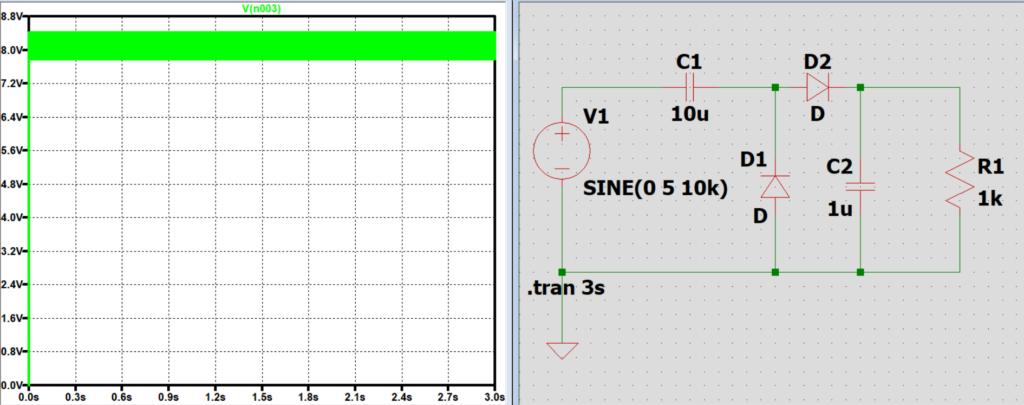
C2は電圧保障の役割があるため、電源やC1から電圧がかかっていない時、
負荷に電源やC1から充電した約2Vm分の電圧を掛けている。
C2の静電容量が小さくなるとこの放電時間が短くなり、負荷に電圧が掛かる時間が短くなり電圧の振れ幅が大きくなってしまう。
C2の静電容量を大きくすると放電時間が長くなるため、次に電源やC1から2Vm分の電圧を掛けるまでの間、
負荷に2Vm分の電圧を掛け続けてくれるため、結果として負荷に掛かる電圧の振れ幅が小さくなる。
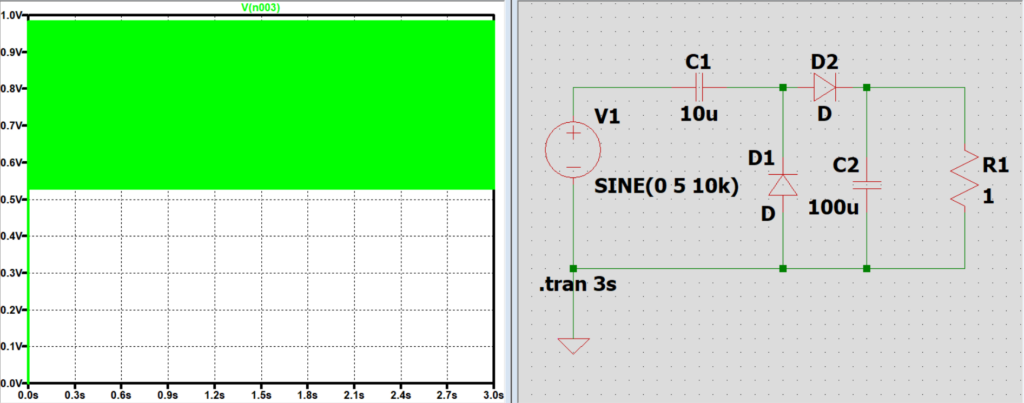
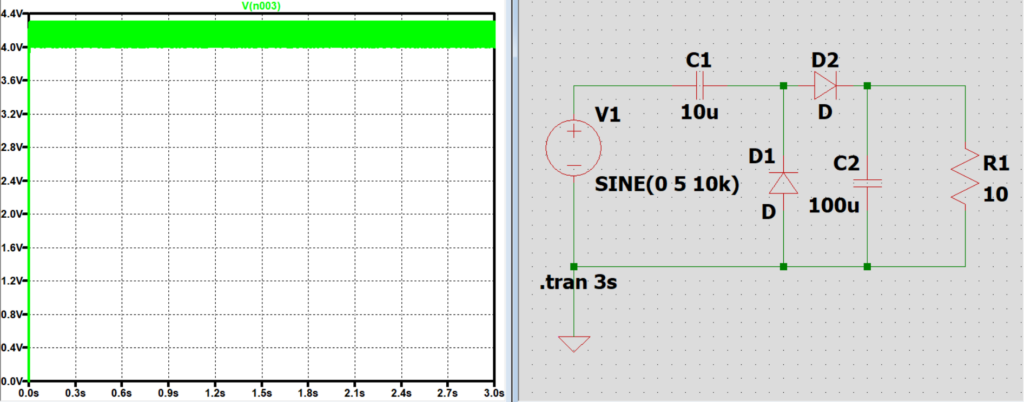
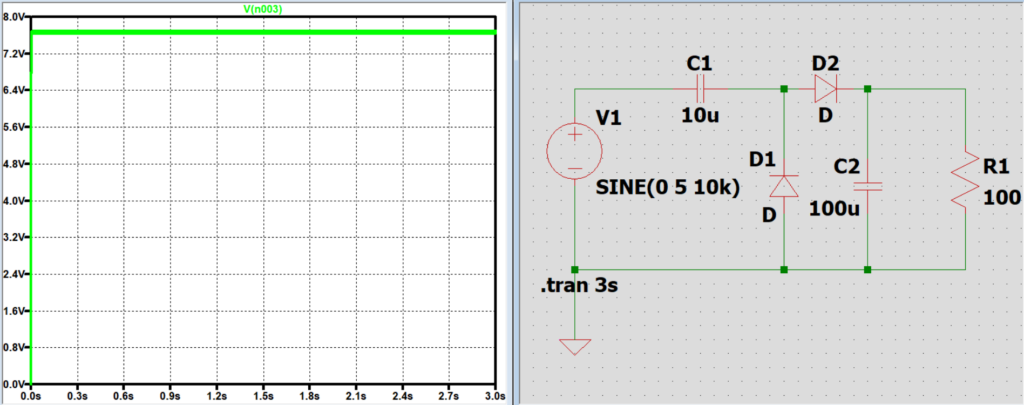
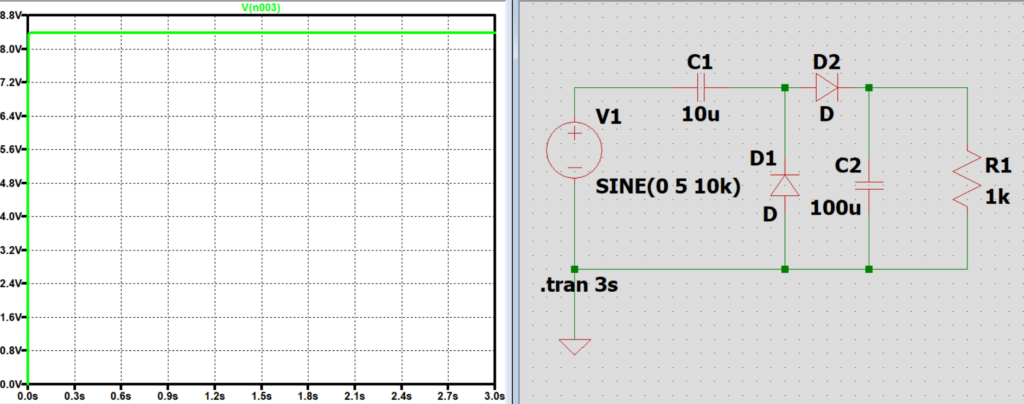
負荷抵抗Rと出力電圧の関係
負荷抵抗Rを大きくなるとRに流れる電流が小さくなり、
放電しきるまでの時間が長くなるため負荷に掛かる電圧の振れ幅が小さくなる。
また、Rが大きくなることでインピーダンスが大きくなるので分圧によりかかる電圧が大きくなる。
倍電圧整流回路の設計手順
①使用する電源の周波数を確認する。
倍電圧整流回路を使用する商用電源の周波数もしくは倍電圧整流回路を接続する元の回路の周波数を把握しておく。
➁負荷に掛ける電圧・負荷に流す電流・電圧変動量(リップル電圧)を決める
電圧を何Vにしたいか、負荷にどれくらい電流を流したいか、許容変動量(リップル電圧)を決めておく。
③コンデンサC2の静電容量を計算する
安定した回路に必要なC2の静電容量を計算する。
\(C2≧\frac{\ I_{load}}{2f×ΔV}\)
※\(\ I_{load}:➁で決定した負荷電流値\)
※ΔV:➁で決定した許容電圧変動量
※f:①で確認した倍電圧整流回路の接続元の回路または商用電源周波数の周波数
④コンデンサC1の静電容量を計算する
安定した回路に必要なC1の静電容量を計算する。
\(C1≧\frac{\ I_{load}×T}{ΔV}\)
※\(\ I_{load}:➁で決定した負荷電流値\)
※ΔV:➁で決定した許容電圧変動量
※T:コンデンサが放電する時間(秒)→通常はT=\(\frac{1}{2f}\)
※f:①で確認した倍電圧整流回路の接続元の回路または商用電源周波数の周波数
⑤コンデンサC2の選定を行う
まず、④で求めた静電容量で⓪の周波数が共振周波数となるコンデンサを選定する。
その後、最大定格も満たす必要がある。主に耐圧を考慮する。
\(\ V_{C2MAX}≧\sqrt{2}×\ V_{AC RMS}×安全率\)
※\(\ V_{AC RMS}:入力電圧の実効値\)
※安全率:定格値に余裕を持たせるために計算結果に掛ける値(基本1.5~2倍程度)
⑥コンデンサC1の選定を行う
まず、④で求めた静電容量で⓪の周波数が共振周波数となるコンデンサを選定する。
その後、最大定格も満たす必要がある。主に耐圧を考慮する。
\(\ V_{C1MAX}≧\sqrt{2}×\ V_{AC RMS}×安全率\)
※\(\ V_{AC RMS}:入力電圧の実効値\)
※安全率:定格値に余裕を持たせるために計算結果に掛ける値(基本1.5~2倍程度)
⑦ダイオードD1とD2の選定を行う。
整流用のダイオードD1とD2は主に以下のパラメータから選定する。
| 項目名 | 意味 | 設計上のポイント |
|---|---|---|
| 逆耐圧(VRRM) | ダイオードが逆方向に耐えられる 最大電圧 | 入力電圧のピーク×2倍以上必要 |
| 順方向電流(IF) | 流し続けられる最大電流 | 負荷電流より余裕を持って大きく |
| 逆回復時間(trr) | スイッチング時の回復速度 | 周波数が高い場合(kHz以上)は短いものを選ぶ |
1.逆耐圧VRRMを計算する
ダイオードが逆方向に耐えられる最大電圧を計算する。
VRRM≧2×\(\sqrt{2}×\ V_{AC RMS}×安全率\)
※\(\ V_{AC RMS}:入力電圧の実効値\)
※安全率:定格値に余裕を持たせるために計算結果に掛ける値(基本1.5~2倍程度)
2.順方向電流IFを計算する
回路で必要な電流は負荷Rによって決まりますが、ダイオードにかかる電流はパルス的であるため、平均電流よりも大きくなる可能性があります。そのため負荷電流×1.5~2倍の順方向電流に耐えれるように計算する。
IF≧1.5~2×\(\ I_{load}\)
3.逆回復時間を計算する
商用電源に接続する場合は周波数は低いので一般整流用ダイオードで問題ない。
高周波スイッチング電源に接続する場合はns程度の回復時間が必要なのでUFシリーズやショットキーにする。
周波数が50/60Hz程度の倍電圧回路 → 遅くてOK(1N400xなどの整流用)
高周波スイッチング電源(kHz以上) → 高速ダイオード(UFシリーズやショットキー)