半導体のジャンクション温度計算とヒートシンク設計

こちらでは半導体のジャンクション温度についての計算方法を解説いたします。
半導体の種類や参照する値によって計算方法が異なってきますので場合別でご紹介いたします。
どの熱モデルを使うかは放熱経路で決定しましょう（SMDは θJB/θJA、TO-220/TO-247は θJC＋ヒートシンク）

面実装ダイオード・(SMD)の場合

面実装ダイオードの場合は基板材質や実際の銅パターンやスルーホール密度で θJA が大きく変化するため、
実機の基板温度を実測して計算するパターン➁を利用すると精度のよい計算を行うことが可能です。

パターン①　Rth(j-a)：ジャンクション-空気間熱抵抗を用いた熱計算

周囲温度とジャンクション-空気間熱抵抗を用いてジャンクション温度を求める際の計算方法

Tj＝Ta+Rth(j-a)×P＝Ta+Rth(j-a)×(VF×IF)
※Tj：ジャンクション温度
※Ta：周囲温度(使用する環境の温度)
※Rth(j-a)：ジャンクション-空気間熱抵抗
※P：ダイオードの消費電力
※VF：ダイオードの順方向電圧
※IF：ダイオードに流れる順方向電流

実際の値を用いた計算例

Tj＝40+60×(0.8×1.0)＝88℃

上記がダイオードの定格温度Tj(今回は150℃)に対して、×0.7倍程度(105℃)以下で、マージンを取れているのでOK

パターン➁ Rth(j-b)：ジャンクション-基板間熱抵抗を用いた熱計算

この式は、主熱流経路が“半導体 → パッケージ → はんだ／リード → 基板 → 空気”というルートが支配的で、かつ他の熱流路（例えばパッケージ表面→空気）を無視または補助経路として小さいと見なせる場合に近似有効です。
この計算方法を使用する時の条件・注意点がありますので下記に記載いたします。

条件 / 注意点	理由 / 補足
他の熱流経路（ケース表面→空気など）が無視できるか小さい	そうでないと実際の (Tj -Tb) は複数経路寄与を含むため、この単純なルートモデルが破綻する
(Tb) の測定点が適正に定義されている	どの基板点温度か（リード付近、ランド近傍、スルーホール近傍等）で取るかで意味が変わる
Rth(j-b)が実機実装条件（銅パターン、ビア、層構成、スルーホール、銅厚など）に近い条件で決まっていること	データシートのRth(j-b) 値は JEDEC 標準 PCB 条件下で測定されることが多く、実基板との乖離が生じうる
定常解析前提	時変損失やパルス動作では過渡熱挙動を考慮する必要がある

基板温度とジャンクション-基板間熱抵抗を用いてジャンクション温度を求める際の計算方法

Tj＝Tb+Rth(j-a)×P＝Tb+Rth(j-b)×(VF×IF)
※Tj：ジャンクション温度
※Tb：基板上（ボード、Board）近傍の温度。パッケージ直下のランドやバーンパッド近傍、もしくはリードピン近傍の基板（銅層）表面温度を指すことが多い。
※Rth(j-b)：ジャンクション-基板間熱抵抗
※P：ダイオードの消費電力
※VF：ダイオードの順方向電圧
※IF：ダイオードに流れる順方向電流

実際の値を用いた計算例(TI：MMBZxxVAL Dual Channel Zener Diode datasheet)

Tj＝60+74.1×(27×0.005)≒70℃

上記がダイオードの定格温度Tj(今回は150℃)に対して、×0.7倍程度(105℃)以下で、マージンを取れているのでOK

リード型ダイオードの場合

放熱の主経路がリード→はんだ→基板/空気”ならパターン➁③ が実態に即しています。
パターン①でもそれなりの精度の計算はできます。

パターン①　Rth(j-a)：ジャンクション-空気間熱抵抗を用いた熱計算

周囲温度とジャンクション-空気間熱抵抗を用いてジャンクション温度を求める際の計算方法

Tj＝Ta+Rth(j-a)×P＝Ta+Rth(j-a)×(VF×IF)
※Tj：ジャンクション温度
※Ta：周囲温度(使用する環境の温度)
※Rth(j-a)：ジャンクション-空気間熱抵抗
※P：消費電力
※VF：ダイオードの順方向電圧
※IF：ダイオードに流れる順方向電流

実際の値を用いた計算例

Tj＝40+60×(0.8×1.0)＝88℃

上記がダイオードの定格温度Tj(今回は150℃)に対して×0.7倍程度(105℃)以下で、マージンを取れているのでOK

パターン➁　Rth(j-l)ジャンクション-リード間熱抵抗を用いた熱計算

ジャンクション-リード間熱抵抗を用いてジャンクション温度を求める際の計算方法

Tj＝TL+Rth(j-l)×P＝TL+Rth(j-l)×(VF×IF)
※Tj：ジャンクション温度
※TL：リードの最熱側はんだ直近のリード温度の実測値(測温点はRth(j-l)の定義に合うリード位置)
※Rth(j-l)：ジャンクション-リード間熱抵抗
※P：消費電力
※VF：ダイオードの順方向電圧
※IF：ダイオードに流れる順方向電流

実際の値を用いた計算例(NTE：nte585)

Tj＝80+15×(0.45×1.5)≒90.1℃

上記がダイオードの定格温度Tj(今回は125℃)に対して×0.7倍程度(87.5℃)以上のため気を付けること。

パターン③　ジャンクション-はんだ間熱抵抗を用いた熱計算

Tj＝Ts+Rth(j-s)×P＝Ts+Rth(j-s)×(VF×IF)
※Tj：ジャンクション温度
※Ts：はんだ点温度の実測(ソルダージョイントに極小熱電対を直付け)
※Rth(j-l)：ジャンクション-リード間熱抵抗
※P：消費電力
※VF：ダイオードの順方向電圧
※IF：ダイオードに流れる順方向電流

実際の値を用いた計算例(DIODES INC：(PDS5100H-13) )

Tj＝70+2.0×(0.1×5.0)＝71.0℃

上記がダイオードの定格温度Tj(今回は175℃)に対して×0.7倍程度(122.5℃)以下で、マージンを取れているのでOK

トランジスタ(スイッチング)の場合

パターン①　Rth(j-a)：ジャンクション-空気間熱抵抗を用いた熱計算

スイッチングしているトランジスタの消費電力は導通損とベース損の合計をデューティー比(ON/OFFの比率)で計算したものにスイッチング損を合計することで計算できます。

消費電力の計算方法は下記になります。

消費電力P＝(Pcont+Pb)・Duty+Psw
導通損Pcont=\(\ (\V_{CE}・Ic)\)
ベース損Pb=\(\ (\V_{BE}・Ib)\)
スイッチング損Psw=\(\ frac{1}{2}VI(tr+tf)f\)
※\(\ V_{CE}：コレクタ-エミッタ間電圧\)
※Ic：コレクタ電流
※\(\ V_{BE}：ベース-エミッタ間電圧\)
※Ib：ベース電流
※tr：立ち上がり時間
※tf：立下り時間
※f：スイッチング周波数
※Duty：デューティー比

ジャンクション温度は以下のように計算できます。

Tj＝Ta+Rth(j-a)×P
※Tj：ジャンクション温度
※Ta：周囲温度(使用する環境の温度)
※Rth(j-a)：ジャンクション-空気間熱抵抗
※P：上記より求めたトランジスタの消費電力

実際の値を用いた計算例(オンセミコンダクター：2N3904)

まずトランジスタの消費電力を求める。

消費電力P＝(Pcont+Pb)・Duty＝(0.035+0.010)×0.5＝0.0225W
導通損Pcont=0.35×0.10＝0.035W
ベース損Pb=1.0×0.010＝0.010W
スイッチング損Psw=\(\ frac{1}{2}VI(tr+tf)f\)≒mW級のため今回は省略

上記よりジャンクション温度は以下となる。

Tj＝40+200×0.0225＝44.5℃

上記がトランジスタの定格温度Tj(今回は150℃)に対して×0.7倍程度(105℃)以下で、マージンがあるためOK

トランジスタ(電流増幅用途）

電流増幅用途でトランジスタを使用している際はトランジスタが電圧を調整しながら電流をながすため、
トランジスタ内で常に電圧降下VCEが発生しているため、導通損が消費電力になります。
また、上記理由より、消費電力はとても大きいため、ヒートシンクの取り付けが必須となります。

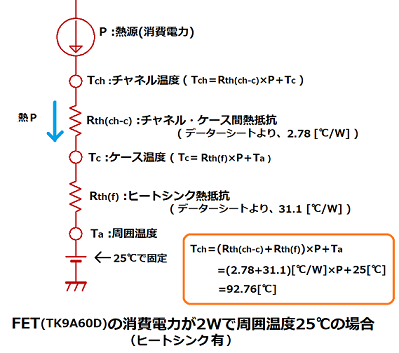
パターン①　Rth(j-c)：ジャンクション-ケース間熱抵抗を用いた熱計算

消費電力の計算方法は下記になります。

消費電力P＝VCE×Ic＝(Ve-Vc)×Ic

※VCE：コレクタエミッタ間電圧(エミッタ電圧Veとコレクタ電圧Vcの差分でも求めることが可能)
※Ic：コレクタ電流
※Ve：エミッタ電圧(トランジスタの入力電圧)
※Vc：コレクタ電圧(トランジスタの出力電圧)

ジャンクション温度は以下のように計算できます。

Tj＝Ta+(Rth(j-c)+Rth(c-s)+Rth(s-a))×P
※Tj：ジャンクション温度
※Ta：周囲温度(使用する環境の温度)
※Rth(j-c)：ジャンクション-ケース間熱抵抗
※Rth(c-s)：ケース-ヒートシンク間熱抵抗
※Rth(s-a)：ヒートシンク-空気間熱抵抗
※P：上記より求めたトランジスタの消費電力

実際の値を用いた計算例(オンセミコンダクター：TIP120)

まずトランジスタの消費電力を求める。

消費電力P＝(12-6)×2.0＝12W

上記よりジャンクション温度は以下となる。

Tj＝40+(1.92+1.78+3.0)×12=120.4℃

上記がトランジスタの定格温度Tj(今回は150℃)に対してマージンがあるが、少しぎりぎりのため、放熱対策などを向上させることも考える。

MOSFET(スイッチ用途)の場合

パターン①　Rth(j-a)：ジャンクション-空気間熱抵抗を用いた熱計算

周囲温度とジャンクション-空気間熱抵抗を用いてジャンクション温度を求める際の計算方法

MOSFETの消費電力は導通損・スイッチング損・ゲート駆動損の合計でを計算できます。
計算方法は下記になります。

消費電力P＝Pcond+Psw+Pg
導通損Pcond＝\(\ I^2rms・\ R_{DS}(on)\)
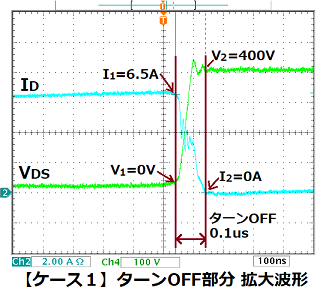
スイッチング損Psw≒\(\frac{1}{2}VDS×\ Isw(tr+tf)fs\)
ゲート駆動損Pg＝Qg×Vg×fs
※\(\ I^2rms\)：
※\(\ R_{DS}(ON)\)：オン抵抗
※VDS：ドレインーソース間電圧(電源電圧や負荷電圧などの電圧。12V電源をスイッチングするなら12V)
※Isw：スイッチング電流
※tr：スイッチングの立ち上がり時間
※tf：スイッチングの立下り時間
※fs：スイッチング周波数
※Qg：総ゲート電荷(1スイッチング当たりの充放電量)
※Vg：ゲート電圧

ジャンクション温度は以下のように計算できます。

Tj＝Ta+Rth(j-a)×P
※Tj：ジャンクション温度
※Ta：周囲温度(使用する環境の温度)
※Rth(j-a)：ジャンクション-空気間熱抵抗
※P：上記で求めたMOSFETの消費電力

実際の値を用いた計算例(TI：CSD18540Q5B)

まず消費電力を求める。

消費電力P＝Pcond+Psw+Pg=0.115+0.288+0.205≒0.61
導通損Pcond＝\(\ I^2rms・\ R_{DS}(on)＝\ 8.0^2×0.0018＝0.115W \)
スイッチング損Psw≒\(\frac{1}{2}V×Isw(tr+tf)fs =\frac{1}{2}\)VI(9n+3n)=0.288W\)
ゲート駆動損Pg＝Qg×Vg×fs=0.000000041×10×500000=0.205W

上記より、ジャンクション温度は以下のようになる。

Tj＝40+0.61×50＝70.5℃

上記がMOSFETの定格温度Tj(今回は175℃)に対して×0.7倍程度(122.5℃)以下で、マージンを取れているのでOK

IGBT(スイッチ用途)の場合

パターン①　Rth(j-c)：ジャンクション-ケース間熱抵抗を用いた熱計算

周囲温度とジャンクション-空気間熱抵抗を用いてジャンクション温度を求める際の計算方法

IGBTの消費電力は導通損とスイッチング損の合計でを計算できます。
計算方法は下記になります。

実際の値を用いた計算例

リニアレギュレータの場合

リニアレギュレータはその性質上熱消費が大きい素子になるため基本的にはパターン➁での設計となる。

パターン①　Rth(j-a)：ジャンクション-空気間熱抵抗を用いた熱計算

周囲温度とジャンクション-空気間熱抵抗を用いてジャンクション温度を求める際の計算方法

リニアレギュレータの消費電力はドロップ電力と静止電流による電力の合計で計算できます。
計算方法は下記になります。

消費電力P＝(Vin-Vout)×Iout+Vin×Iq
※Vin：リニアレギュレータの入力電圧
※Vout：リニアレギュレータの出力電圧
※Iout：リニアレギュレータの出力電流
※Iq：リニアレギュレータの静止電流

ジャンクション温度は以下のように計算できます。

Tj＝Ta+Rth(j-a)×P
※Tj：ジャンクション温度
※Ta：周囲温度(使用する環境の温度)
※Rth(j-a)：ジャンクション-空気間熱抵抗
※P：上記より求めたリニアレギュレータの消費電力

実際の値を用いた計算例(TI：LM340、LM7805)

まずリニアレギュレータの消費電力を求める。

消費電力P＝(12-5)×0.5+12×0.008＝3.596W

上記よりジャンクション温度は以下となる。

Tj＝40+23.9×3.596＝125.9℃

上記がリニアレギュレータの定格温度Tj(今回は150℃)に対して×0.7倍程度(105℃)以上で、マージンがないため、
ヒートシンクを取り付けて設計することを推奨する。

パターン➁　Rth(j-c)：ジャンクション-ケース間熱抵抗を用いた熱計算(ヒートシンク使用

ヒートシンクとジャンクション-ケース間熱抵抗を用いてジャンクション温度を求める際の計算方法

リニアレギュレータの消費電力はドロップ電力と静止電流による電力の合計で計算できます。
計算方法は下記になります。

消費電力P＝(Vin-Vout)×Iout+Vin×Iq
※Vin：リニアレギュレータの入力電圧
※Vout：リニアレギュレータの出力電圧
※Iout：リニアレギュレータの出力電流
※Iq：リニアレギュレータの静止電流

ジャンクション温度は以下のように計算できます。

Tj＝Ta+(Rth(j-c)+Rth(c-s)+Rth(s-a))×P
※Tj：ジャンクション温度
※Ta：周囲温度(使用する環境の温度)
※Rth(j-c)：ジャンクション-ケース間熱抵抗
※Rth(c-s)：ケース-ヒートシンク間熱抵抗
※Rth(s-a)：ヒートシンク-空気間熱抵抗
※P：上記より求めたリニアレギュレータの消費電力

実際の値を用いた計算例(TI：LM340、LM7805)

まずリニアレギュレータの消費電力を求める。

消費電力P＝(12-5)×0.5+12×0.008＝3.596W

上記よりジャンクション温度は以下となる。

Tj＝40+(1.7+1.78+3.0)×3.596＝63.3℃

上記がリニアレギュレータの定格温度Tj(今回は150℃)に対して×0.7倍程度(105℃)以下で、マージンを取れているのでOK

スイッチングレギュレータ(DC-DCコンバータIC)の場合

スイッチング電源 IC は銅面放熱が支配しているため パターン➁（Rth(j-b)＋基板温度Tb）のほうが実情に近い場合が多いです。
精密にやるなら、内蔵 FET の オン抵抗（HS 148 mΩ、LS 78 mΩ）、スイッチング周波数 500 kHz 等を使ってMOSFETとゲート損の個別見積りに展開します（数値は DS 参照）。TI

パターン①　Rth(j-a)：ジャンクション-空気間熱抵抗を用いた熱計算

周囲温度とジャンクション-空気間熱抵抗を用いてジャンクション温度を求める際の計算方法

DC-DCコンバータICの消費電力はチップ内訳（HS/LS FET の導通＋スイッチング＋ゲート・駆動や損失）を積み上げてもよいですが、まずは効率ηから素早く求めるのが実務的です。

消費電力\(\ P＝Pout(\frac{1}{η}-1)\)
Pout＝Vout×Iout
※Pout：DC-DCコンバータICの出力消費電力
※η：DC-DCコンバータICの効率
※Vout：DC-DCコンバータICの出力電圧
※Iout：DC-DCコンバータICの出力電流

ジャンクション温度は以下のように計算できます

Tj＝Ta+Rth(j-a)×P
※Tj：ジャンクション温度
※Ta：周囲温度(使用する環境の温度)
※Rth(j-a)：ジャンクション-空気間熱抵抗
※P：上記より求めたDC-DCコンバータICの消費電力

実際の値を用いた計算例(TI：TPS54202)

まずはDC-DCコンバータICの消費電力を求める。

消費電力\(\ P＝7.5(\frac{1}{0.92}-1)＝0.65W\)
Pout＝5×1.5＝7.5W

上記よりジャンクション温度は以下となる。

Tj＝40+89.2×0.65＝98.0℃

上記がダイオードの定格温度Tj(今回は150℃)に対して×0.7倍程度(105℃)以下で、マージンを取れているのでOK

パターン➁ Rth(j-b)：ジャンクション-基板間熱抵抗を用いた熱計算

基板温度とジャンクション-基板間熱抵抗を用いてジャンクション温度を求める際の計算方法

DC-DCコンバータICの消費電力はチップ内訳（HS/LS FET の導通＋スイッチング＋ゲート・駆動や損失）を積み上げてもよいですが、まずは効率ηから素早く求めるのが実務的です。

消費電力\(\ P＝Pout(\frac{1}{η}-1)\)
Pout＝Vout×Iout
※Pout：DC-DCコンバータICの出力消費電力
※η：DC-DCコンバータICの効率
※Vout：DC-DCコンバータICの出力電圧
※Iout：DC-DCコンバータICの出力電流

ジャンクション温度は以下のように計算できます

Tj＝Tb+Rth(j-b)×P
※Tj：ジャンクション温度
※Tb：基板温度(デバイス直下の基板近傍温度（ランド/露出PAD付近など、メーカー定義に近い測温点）)
※Rth(j-ｂ)：ジャンクション-基板間熱抵抗
※P：上記より求めたDC-DCコンバータICの消費電力

実際の値を用いた計算例(TI：TPS54202)

まずはDC-DCコンバータICの消費電力を求める。

消費電力\(\ P＝7.5(\frac{1}{0.92}-1)＝0.65W\)
Pout＝5×1.5＝7.5W

上記よりジャンクション温度は以下となる。

Tj＝60+14.7×0.65＝69.6℃

上記がダイオードの定格温度Tj(今回は150℃)に対して×0.7倍程度(105℃)以下で、マージンを取れているのでOK

オペアンプの場合

パターン①　Rth(j-a)：ジャンクション-空気間熱抵抗を用いた熱計算

周囲温度とジャンクション-空気間熱抵抗を用いてジャンクション温度を求める際の計算方法

オペアンプの消費電力は静止電流による損失と出力段の損失の合計でを計算できます。
計算方法は下記になります。

消費電力P＝Pq+Ps
Pq＝Vs×Icc×ch
Ps＝(VS-Vout)・Iout
※Pq：静止電流による消費電力
※Ps：出力段の損失(デバイス内部で消費される電力)
※ch：チャネルの本数
※Vs：オペアンプの電源電圧
※Icc：オペアンプの静止電流
※Vout：オペアンプの出力電圧
※Iout：オペアンプの出力電流

上記よりジャンクション温度は以下となる。

Tj＝Ta+Rth(j-a)×P
※Tj：ジャンクション温度
※Ta：周囲温度(使用する環境の温度)
※Rth(j-a)：ジャンクション-空気間熱抵抗
※P：上記で求めたオペアンプの消費電力

実際の値を用いた計算例(TI：LM358B(D(SOIC)))

まずはオペアンプの消費電力を求める。

消費電力P＝0.0072+0.035＝0.0422W
Pq＝12×0.0003×2＝0.0072W
Ps＝(12-5)・0.005＝0.035W

上記よりジャンクション温度は以下となる。

Tj＝40+124.7×0.0422＝45.3℃

上記がダイオードの定格温度Tj(今回は150℃)に対して×0.7倍程度(105℃)以下で、マージンを取れているのでOK

必要ヒートシンク温度の計算方法

1. 損失P、TA（最悪高温）を確定。
2. データシートの**TJ(max)**から必要温度差ΔT = TJ(max) − TA（≧必要余裕）を定義。
3. パッケージθJCを採用。ψJTはヒートシンク設計に使わない。(TI E2E)
4. 予定のTIMのθCS（または熱抵抗/熱伝導率×厚み/面積で換算）を見積。
5. 必要な**θSA(req)**を逆算：
   θSA(req) = ΔT/P − (θJC + θCS)。
6. ヒートシンクカタログのθSA-風量-姿勢データから候補選定（自然/強制対流で大きく変わる）。(ボイドコーポレーション)
7. 取り付けねじ/クランプ圧・界面処理でθCS実力を確保。
8. 試作実測：TC, TT, Tfin, TA、風量、Pを測定し、TJ = TC + P·θJC（※θJCの定義に沿う測温点が必要、メーカーの定義に従う）や、熱カメラ/埋込熱電対で検証。(ROHM)

必要θSAは θSA(req) = (TJ(max)−TA)/P − (θJC+θCS) で逆算し、風量・姿勢・TIM実力で最悪側再計算。(ボイドコーポレーション)

仮定）

• デバイス：TO-220相当、θJC = 2.0 ℃/W（DS値）
• 損失：P = 10.0 W
• 環境：TA = 40 ℃（筐体内）
• 目標：TJ ≤ 125 ℃
• TIM：シリコーンシート 0.2 ℃/W（組立後見込み）

(1) ヒートシンク必要条件
ΔT = TJ(max) − TA = 125 − 40 = 85 ℃
許容総熱抵抗（J→A）= ΔT / P = 85 / 10 = 8.5 ℃/W
θJC + θCS = 2.0 + 0.2 = 2.2 ℃/W
よって必要ヒートシンク：
θSA(req) = 8.5 − 2.2 = 6.3 ℃/W 以下（自然空冷で到達できる寸法か要検討）。(ボイドコーポレーション)

---

---

---

---

---

---